数値計算の足跡
このページは何?
私が所属する研究室では数値計算(特に磁気流体シミュレーション)による研究が盛んです。私も数値計算を勉強している最中ですが、自分が勉強してきたことを後から眺めることが
できるような場所が欲しいなと思い、このようなページを作りました。基本的に自分のために作ったページですが、後から数値計算を勉強する方々も参考にしていただければ
と思います。
数値積分
ある関数が与えられたとき、それを不定積分した結果は一般には初等関数で表すことはできない。解析的に積分できないものは、コンピュータを用いて計算するしかない。
今回は、1変数関数の定積分
$$ \int_{a}^{b} f(x) dx $$
の計算方法を解説する。コンピュータは離散化された数値しか扱えないため、積分領域を有限個に分割し、それぞれの区間における関数の値の和を求めることで定積分値を出すしかない。
一番簡単な方法は、長方形の短冊に分割してその和をとるという方法である。すなわち
$$ \sum_{i=0}^{N} f(a + i \cdot \Delta x) \cdot \Delta x $$
を計算するのである。ここで$N$はメッシュ数で、$\Delta x N = b-a$の関係を満たしている。この式において、$\Delta x$が0に近づく極限が積分の定義なのであるから、
当然ながら$\Delta x$が小さいほど正確な値が得られる。その代わり、
$\Delta x$を小さくするとその分$N$が大きくなり、計算量が増えてしまう。精度と計算量はトレードオフの関係なのだ。
ところが、計算量を変えずに精度を上げる方法がある。それは「アルゴリズムを変える」こと。専門用語で「高次精度化」とも呼ばれる。例えば、先ほどは長方形の短冊
に分割して計算したが、これを細い台形に分割して計算したらどうなるだろうか。詳細は省くが、台形による近似をすると
$$ \sum_{i=0}^{N} f(a + i \cdot \Delta x) \cdot \Delta x - \frac{f(a)+f(b)}{2} $$
という形で積分値を求めることができる。長方形で近似したときの式に少し定数項が加わるだけである。なんとこれだけで計算の精度が上がるのである。どれだけ精度が
良くなるかというと、長方形近似の場合は「メッシュを10倍細かくすると誤差が1/10になる」程度(これを1次精度と呼ぶ)であるが、台形近似の場合は
「メッシュを10倍細かくすると誤差が1/100」になる(これを2次精度と呼ぶ)のである。高次精度化は数値計算においてきわめて有用な概念であることをおさえておきたい。
例題として、$\int_{0}^{1} e^{-x^2}dx$を計算してみると、結果は約0.7468であった。
C言語によるソースコードは
こちら
常微分方程式
物理学では、どんな分野であろうと微分方程式が頻出する。微分方程式は通常、解析解を求めるのがとても難しい。そこで、数値計算の出番である。微分方程式の解析解が
分からなくとも、変数がどんな値のときに関数がどんな値をとるのかさえ分かれば定量的な議論ができる。微分方程式を計算するプログラムが書けることは物理をやる上で
非常に大事である。
今回は、最も簡単な微分方程式である常微分方程式の解法について述べる。例題として
$$ \frac{d^2 y}{d x^2} + \frac{2}{x} \frac{dy}{dx}+ y^2 = 0 ,\ \ y(x=0) = 1,\ \ y'(x=0)=0$$
を解いてみよう。ここで$x$は独立変数で、$y$は$x$に依存する関数である。この方程式には$y$の1階微分・2階微分が含まれるが、数値計算においては例え同じ関数でも
微分の階数が異なるものは別の変数とみなし、連立方程式のように同時に解くのが基本である。今回の方程式を離散化するために、$x$の刻み幅を$dx$、$y$の1階・2階微分
をそれぞれ$dy, ddy$とおこう。すると元の方程式は次のような連立方程式に置き換えられる。
$$ ddy = -\frac{2}{x}dy - y^2 \ \ \ (1)$$
$$ dy_{\rm{new}} = dy + ddy \cdot dx \ \ \ (2)$$
$$ y_{\rm{new}} = y + dy \cdot dx \ \ \ (3)$$
ただし$y_{\rm{new}}, dy_{\rm{new}}$は$x$を少し増やしたときの$y, dy$の値を表す。計算のアルゴリズムは以下で良さそうだ。
[1] 変数$x, dx, y, dy, ddy$を定義する。$x=0$の初期条件が分かっているので、$x=0, \ y=1,\ dy=0$をセット。$dx$は適当に決めておく。
[2] (1)式により、2階微分$ddy$の値を決定。
[3] (2)(3)式より、$y, dy$を更新。このとき$x$を$dx$だけ増やす。
[4] $x,y$の値をテキストファイルに出力。
[5] 計算したい分だけ[2][3][4]を繰り返す。
一つ注意したいのが、このアルゴリズムでは一次の精度しか出ないということである。ただし、高次精度化をするにしても[2]のパートがやや複雑になるだけで、基本はこの
アルゴリズムで計算できる。高次精度の微分方程式の解法を知りたい方は、「ルンゲクッタ法」などで検索してみるのが良いだろう。
ルンゲクッタ法を用いてこの微分方程式を計算し、gnuplotで$y=y(x)$の概形を書くと以下のようになった。
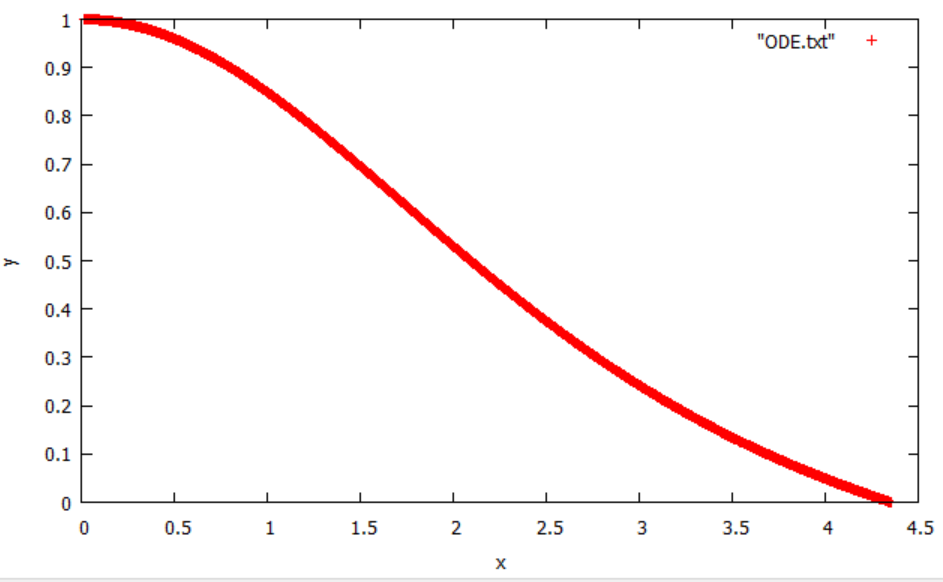
C言語によるソースコードは
こちら
拡散方程式
初期条件・境界条件が与えられた拡散方程式
$$ \frac{\partial u}{\partial t} = a \frac{\partial^2 u}{\partial x^2} ,\ \ u(x>0,t=0)=20,\ \ u(x=0,t)=300 $$
を計算したい。今回は$a=0.8 \rm{[cm^2/t]}$とする。(アルミニウム棒の熱拡散方程式が大体そのくらいの値)
拡散方程式を解くためには、方程式を離散化しなければならない。離散化した微分方程式を「差分方程式」と呼ぶ。差分方程式の立て方は一意ではなく、いくらでもパターンがある。
しかし、拡散方程式に関してはこの差分方程式が一番有名かつ分かりやすいだろう。
$$ \frac{u^{n+1}_{j}- u^{n}_{j}}{\Delta t} = a \frac{u^{n}_{j+1}- 2u^{n}_{j} + u^{n}_{j-1}}{(\Delta x)^2} $$
ここで$u^{n}_{j}$は、時空を離散化した際に位置$j$番目、時間$n$番目にあたる$u$の値(つまり$u(j\Delta x,n\Delta t)$)のことである。
この差分方程式により拡散方程式を解くことを「陽解法」と呼ぶ。なぜ「陽」かというと、時刻$n+1$における$u$の値を、その1つ前の時刻における$u$の値を用いて
$$ u^{n+1}_{j} = f(u^{n}_{j-1},u^{n}_{j},u^{n}_{j+1})$$
というように陽関数として表すことができるからだ。
陽解法のアルゴリズム例を以下に示す。
[1] 空間メッシュ数$N$と同じだけの数の配列$u[0],u[1],...,u[N-1]$を用意する。
[2] 値更新用の配列$u'[0],u'[1],...,u'[N-1]$を用意する。
[3] 初期条件より、$u[0],u[1],...,u[N-1]$に$t=0$における値を代入する。
[4] 差分方程式より、新しい時刻における$u$の値を計算し、$u'[0],u'[1],...,u'[N-1]$に代入する。このとき、$u^{n+1}_{j}$の値を得るのに$u^{n}_{j-1},u^{n}_{j},u^{n}_{j+1}$
の3点の情報が必要なので、端点では特別な処理が必要になる。$u'[0]$は境界条件から得られるが、$u'[N-1]$は$u'[N-2]$と同じ値にするなどして対処することが多い。
[5] $u'[0],u'[1],...,u'[N-1]$の値を$u[0],u[1],...,u[N-1]$にまるごと移し替える。このとき、$u[0],u[1],...,u[N-1]$の値をテキストファイルに出力
[6] 時間が最後まで到達するまで、[4][5]を繰り返す。
このアルゴリズムでは端点$u[N]$より先に物理量が伝搬しないという設定となっているので、無限の長さの棒における熱伝導などを計算したい場合は(計算したい空間スケール)<<$N\Delta x$
となるようにすること。また、陽解法では$\frac{a\Delta t}{(\Delta x)^2}>\frac{1}{2}$のとき誤差が増幅して正しい結果が出ない可能性があるので注意。時間メッシュは空間
メッシュよりも十分細かくとろう。
陽解法による結果は以下の通り。
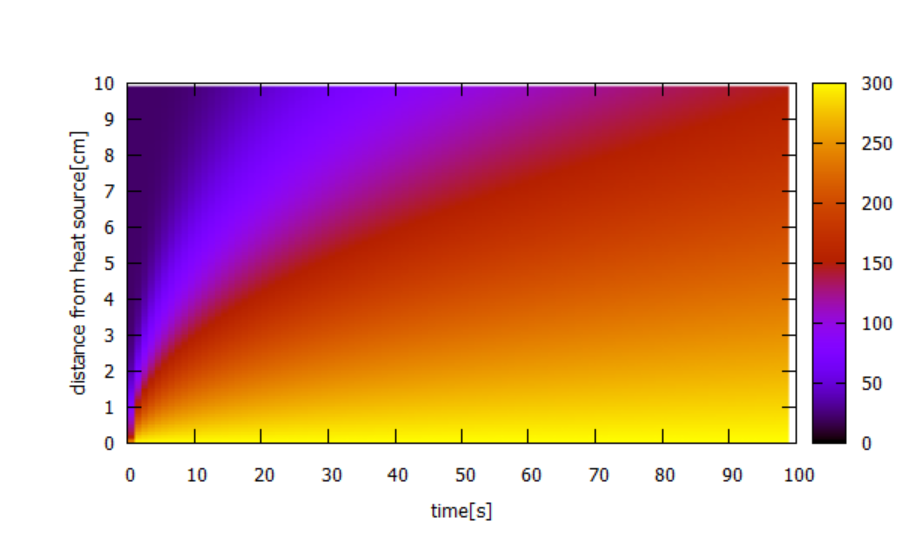
C言語によるソースコードは
こちら
移流方程式
移流方程式
$$ \frac{\partial u}{\partial t} + c\frac{\partial u}{\partial x} = 0,\ \ u(x,t=0)=\exp \left(-\frac{(x-10)^2}{8} \right) $$
を解きたい。今回は$c=1$(無次元)とする。
まず、この微分方程式を差分化する。以下の2次精度の差分化が知られている。
$$u^{n+1}_{j} = u^{n}_{j} - \frac{c\Delta t}{2\Delta x}(u^{n}_{j+1} - u^{n}_{j-1}) + \frac{c^2(\Delta t)^2}{2(\Delta x)^2}(u^{n}_{j+1} -2u^{n}_{j}+ u^{n}_{j-1})$$
あとはこれを計算するだけだが、今回は境界条件が課されていないのでこのままでは端点処理に困る。せっかくなので周期的境界条件を課してみよう。すなわち、$u[0]=u[N-1]$とするのだ。
この条件を課せば$u[0],u[N-1]$の値を差分方程式から問題なく求められる。ただし、初期条件が境界条件に反するようなことがあってはならない。今回の初期条件は$x=10$を中心
としたガウシアンなので、$u(x=0,t)=u(x=20,t)$とするのが良いであろう。
結果は以下の通り。(横軸が$x$座標、縦軸が関数$u(x,t)$の値)
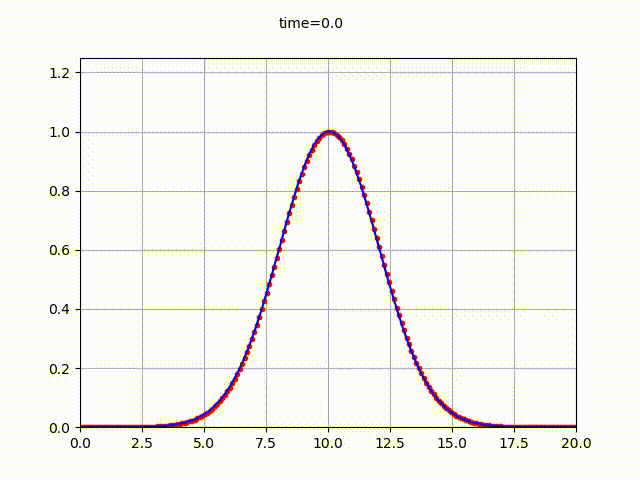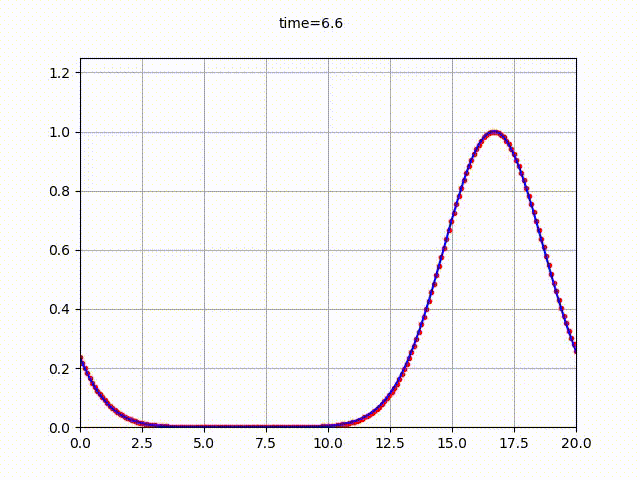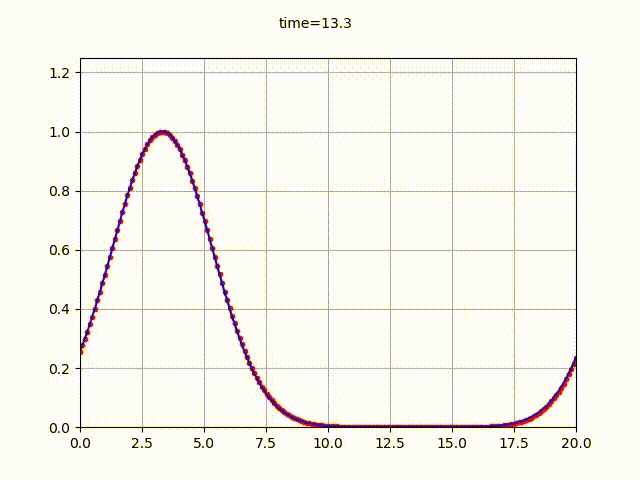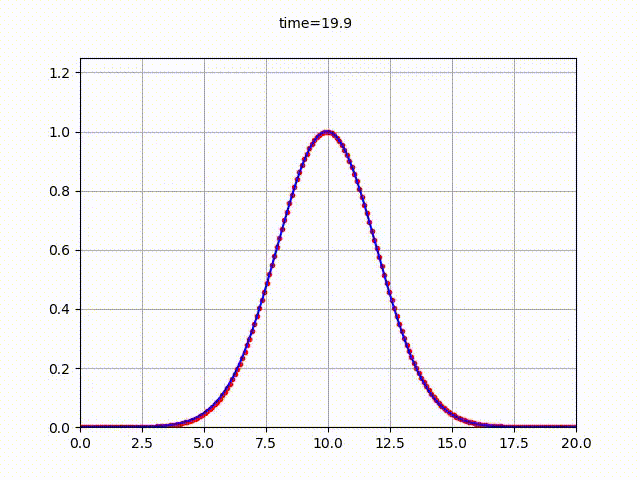
C言語によるソースコードは
こちら
結果をアニメ化するPythonコードは
こちら
流体計算の基礎
拡散方程式や移流方程式の節では、基本的な偏微分方程式の計算方法を学んだ。ここからは連立偏微分方程式である流体の数値計算法について述べる。
一般に流体の方程式は非線形で、変数も多く、計算するのはかなり難しい。それでもまずは簡単なバージョンから少しづつ理解していこう。まずは1次元で粘性がない流体を考える。
このとき、流体を記述する方程式は
$$ \frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x} = 0 $$
$$ \frac{\partial (\rho u)}{\partial t} + \frac{\partial (\rho u^2)}{\partial x} = - \frac{\partial p}{\partial x} $$
$$ \frac{\partial E}{\partial t} + \frac{\partial }{\partial x}\left((E + p)u \right) = 0 ,\ \ E=\frac{p}{\rho (\gamma-1)}$$
の3連立非線形偏微分方程式として記述される。上から順に連続の式、運動方程式、エネルギー式を表す。ここで、エネルギー$E$は理想気体・ポリトロピックの仮定より導出した。
これらの方程式の導出の詳細に関しては、流体力学の本を参考にされたい。
この方程式系は、関数$\rho(x,t), u(x,t), p(x,t)$についての3連立非線形偏微分方程式であり、解くのは容易ではなさそうだ。しかし、この方程式系をシンプルな形に
まとめる方法がある。それは、以下のようなベクトル
$$ \bm{U} = \begin{pmatrix} \rho \\ \rho u \\ E \end{pmatrix} ,\ \ \
\bm{F} = \begin{pmatrix} \rho u \\ \rho u^2 + p \\ u(E+p) \end{pmatrix} $$
を定義することにより
$$ \frac{\partial \bm{U}}{\partial t} + \frac{\partial \bm{F}}{\partial x} = 0 $$
と書き表すことである。さらに、ヤコビアン
$$ A = \frac{\partial {\bm{F}}}{\partial \bm{U}} =
\begin{pmatrix} 0 & 1 & 0 \\ -\frac{(\gamma-3)u^2}{2} & (3-\gamma)u^2 & \gamma-1 \\
-\frac{\gamma uE}{\rho}+(\gamma-1)u^3 & \frac{\gamma E}{\rho}-\frac{3(\gamma-1)u^2}{2} & \gamma u \end{pmatrix}$$
を定義して
$$ \frac{\partial \bm{U}}{\partial t} + A\frac{\partial \bm{U}}{\partial x} = 0 $$
と書くこともできる。これは移流方程式とよく似た形である。行列$A$は速度に対応することになる。実際、$A$の固有値は$u-c_{f},\ u,\ u+c_{f}$である。
ここで$c_{f}$は音速で
$$ c_{f} = \sqrt{\frac{\gamma p}{\rho}} $$
である。
流体の疑似リーマン解法
